5.2 轴对称导学案

概要：3、请你仔细观察点的坐标，你能发现关于坐标轴对称的点的坐标有什么规律吗？4、尝试再找几个点，分别画出它们的对称点。5、小组合作，总结规律在平面直角坐标系中：关于x轴对称的点横坐标相等，纵坐标互为相反数；关于y轴对称的点横坐标互为相反数，纵坐标相等.即：点（x， y）关于x轴对称的点的坐标为(x， - y)；点（x， y）关于y轴对称的点的坐标为(- x， y)。三、巩固新知1、说出下列各点关于x轴、y轴对称的点的坐标：(2，-3)；(-1，2)；(-6，-5)；(0，-1.6)； (4，0)。 2、如下图，△ABC关于x轴对称，点A的坐标为（1，-2），说出点B的坐标。 3、四边形ABCD的四个顶点的坐标分别为A（－5，1）、B（－2，1）、 C（－2，5） 、D（－5，4），分别作出四边形关于x轴与y轴对称的图形。 4、归纳画法（1）求出对称点的坐标；（2）描点；（3）连接点。五、拓展延伸1、分别作出点△ABC关于直线x=1(记为m)和直线y=-1(记为n)对称的图形.2、你能发现它们的对应点的坐标之间分别有什么关系吗? 3、归纳：(1)、点（x，y）

5.2 轴对称导学案,标签：二年级数学课程同步大全,http://www.youer8.com
3、请你仔细观察点的坐标，你能发现关于坐标轴对称的点的坐标有什么规律吗？

4、尝试再找几个点，分别画出它们的对称点。

5、小组合作，总结规律

在平面直角坐标系中：

关于x轴对称的点横坐标相等，纵坐

标互为相反数；关于y轴对称的点横坐标互为相反数，纵坐标相等.

即：点（x， y）关于x轴对称的点的坐标为(x， - y)；点（x， y）关于y轴对称的点的坐标为(- x， y)。

三、巩固新知

1、说出下列各点关于x轴、y轴对称的点的坐标：

(2，-3)；(-1，2)；(-6，-5)；(0，-1.6)； (4，0)。

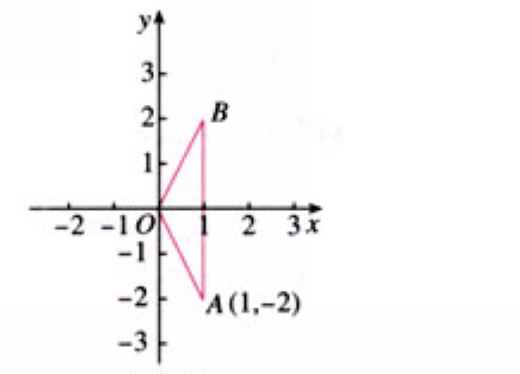
 2、如下图，△ABC关于x轴对称，点A的坐标为（1，-2），说出点B的坐标。

 

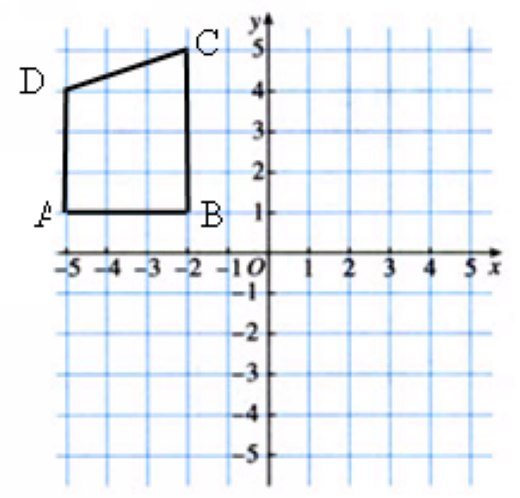
   3、四边形ABCD的四个顶点的坐标分别为A（－5，1）、B（－2，1）、 C（－2，5） 、D（－5，4），分别作

出四边形关于x轴与y轴对称的图形。

 

 4、归纳画法

（1）求出对称点的坐标；

（2）描点；

（3）连接点。

五、拓展延伸

1、分别作出点△ABC关于直线x=1(记为m)和直线y=-1(记为n)对称的图形.

2、你能发现它们的对应点的坐标之间分别有什么关系吗?

 

 

 3、归纳：

(1)、点（x，y）关于直线x=m对称点的坐标是（2m-x，y）.

(2)、点（x， y）关于直线y=n对称点的坐标是（x，2n-y）.

www.youer8.com

六、巩固练习

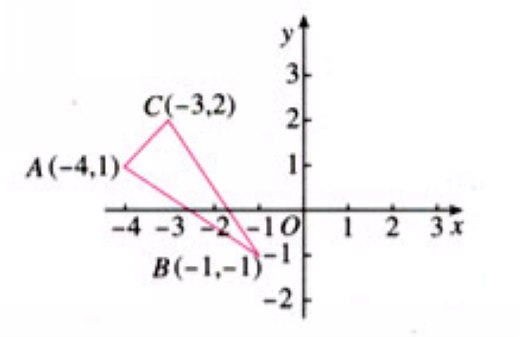
1、如图，利用关于坐标轴对称的点的坐标的特点，分别作出与△ABC关于x轴和y轴对称的图形.

 

 2、已知点P(2a+b，-3a)与点P`(8，b+2).

 （1）若点p与点p`关于x轴对称，则a=_____ b=_______.

（2）若点p与点p`关于y轴对称，则a=_____ b=_______.

三．例题解析

等腰三角形

一．相关知识回顾

1.三角形的分类：按角分为锐角三角形，直角，钝角。

2.轴对称图形：如果一个图形沿一条直线折叠，直线两侧的图形能够互相重合，这个图形就叫做轴对称图形。

3.线段的垂直平分线性质:线段垂直平分线上的点到这条线段两个端点的距离相等。

4.三角形的全等：能够完全重合的两个三角形叫全等三角形。

5.三角形的内角和定理：三角形的内角和为180°。

二．本节知识点

   1.等腰三角形的概念：有两边相等的三角形叫做等腰三角形，其中相等的两边叫腰，另一条边叫底边，两腰所夹的角叫顶角，底边与腰的夹角叫做底角。

   2.等腰三角形的性质：

      （1）等腰三角形的两个地角相等。（等边对等角）

      （2）等腰三角形的顶角平分线，底边上的中线，底边上的高互相重合。（三线合一）

3.等腰三角的判定：如果一个三角形有两个角相等，那么着两个角所对的边也相等。

4.等边三角形的定义：三条边相等的三角形叫做等边三角形。

5.等边三角形的性质：等边三角形的三个内角都相等，并且每个内角都等于60°。

6.等边三角形的判定:

  (1)有等边三角形的定义判定：三边相等的三角形是等边三角形。

（2）三个角都相等的三角形是等边三角形。

（3）有一个角是60°的等腰三角形是等边三角形。

7.含30°角的直角三角形的性质

  在直角三角形中，30°角所对的直角边等于斜边的一半。

三．例题解析

   例1.如图3-1，已知在△ABC中，AB=AC，D在AB上，E在AC的延长线上，且BD=CE，连接DE交BC于F，求证：DF=EF.

1.如图3-2，已知△ABC中，AB=AC，D是CB延长线上的一点，∠ADB=60°，E是AD上的一点，且有DE=DB，求证：AE=BE+BC.

例2.如图3-3，在△ABC中，AD⊥BC于D，∠B=2∠C，求证：AB+BD=CD.

2.如图3-4.已知△ABC中，∠ABC=3∠C，AD是∠BAC的平分线，BE⊥AD于E.求证：2BE=AC-AB.

例3.如图3-5，已知AB=AC，BD⊥AC于D.求证：2∠DBC=∠BAC.

3.如图3-6，，1=∠2，DE//AC，EF⊥AD交BC的延长线于F。试证：∠3=∠B.

运用面积法证明有关的问题

例4.如图3-7已知等边三角形ABC和点P，设P到△ABC三边AB，AC，BC的距离分别为h1，h2，h3，△ABC的高位h。

“若点P在一边BC上，此时h2=0，则可得结论：h1+h2+h3=h（如图（1））”

（1）请直接应用上述信息解决下列问题：

              当点P在△ABC内部(如图2)，点P在△ABC外部（如图（3））这两种情况时，上述结论是否还成立？若成立，请给予证明；若不成立，h1，h2，h3与h之间又有怎样的关系？请写出你的猜想，不用证明。

（2）若不应用上述信息，请探究其他的方法来证明你猜想的结论。

4.如图3-8，△ABC中，AB=AC，D是底边BC上的一点，DM⊥AB，DN⊥AC，垂足

上一页  [1] [2] [3] 

上一篇：5.1东南西北导学案