上海预初第二学期数学知识点（二）

概要：26.方程中的项、系数、次数等概念①项：在方程中，被“+”“-”号隔开的每一部分（含这部分前面的“+”“-”号在内）称为一项②未知数的系数：在一项中，写在未知数前面的数字或表示已知数的字母。③项的次数：在一项中，所有未知数的指数和。④常数项：不含未知数的项。27.列方程的方法列方程：为了求未知数，在未知数和已知数之间建立一种等量关系，就是列方程。列方程步骤：设未知数，找等量关系，列方程。28.方程的解和解方程使方程的左右两边相等的未知数的值叫做方程的解。求方程的解的过程叫做解方程。29.一元一次方程的概念概念：在一个方程中，只含有一个未知数，且未知数的次数是一次的方程。最简形式：ax=b（a不等于0）标准形式：ax+b=0（a不等于0）30.等式的基本性质性质1:等式两边同时加上（或减去）同一个数或同一个代数式，所得结果仍是等式；性质2:等式两边同时乘以同一个数（或除以同一个不为零的数），所得结果仍是等式。另外性质：①对称性：a=b，则b=a;②传递性：若a=b且b=c，

上海预初第二学期数学知识点（二）,标签：六年级数学课程同步大全,http://www.youer8.com

　　26.方程中的项、系数、次数等概念

　　①项：在方程中，被“+”“-”号隔开的每一部分（含这部分前面的“+”“-”号在内）称为一项

　　②未知数的系数：在一项中，写在未知数前面的数字或表示已知数的字母。

　　③项的次数：在一项中，所有未知数的指数和。

　　④常数项：不含未知数的项。

　　27.列方程的方法

　　列方程：为了求未知数，在未知数和已知数之间建立一种等量关系，就是列方程。

　　列方程步骤：设未知数，找等量关系，列方程。

　　28.方程的解和解方程

　　使方程的左右两边相等的未知数的值叫做方程的解。

　　求方程的解的过程叫做解方程。

　　29.一元一次方程的概念

　　概念：在一个方程中，只含有一个未知数，且未知数的次数是一次的方程。

　　最简形式：ax=b（a不等于0）

　　标准形式：ax+b=0（a不等于0）

　　30.等式的基本性质

　　性质1:等式两边同时加上（或减去）同一个数或同一个代数式，所得结果仍是等式；

　　性质2:等式两边同时乘以同一个数（或除以同一个不为零的数），所得结果仍是等式。

　　另外性质：①对称性：a=b，则b=a;②传递性：若a=b且b=c，则a=c（等量代换）

　　31.利用等式的基本性质解一元一次方程

　　解方程：求方程的解的过程。

　　移项法则：方程中任何一项，在改变符号后，从方程的一边移到另一边，这种变形叫移项。

www.youer8.com

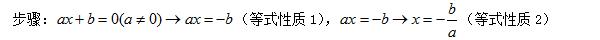
　　32.列方程解应用题步骤

　　审题、设元、列方程、解方程、检验、作答

　　33.按比例分配问题

　　已知两个量之比为a:b，则设这两个量分别为ax和bx.

　　34.利率问题

　　利息=本金×利率×期数

　　本利和=本金+利息=本金×（1+利率×期数）

　　利息税=利息×税率

　　税后利息=利息-利息税=利息×（1-税率）

　　税后本利和=本金+税后利息

　　35.折扣问题

　　利润额=成本价×利润率

　　售价=成本价+利润额

　　新售价=原售价×折扣

　　36.行程问题

　　路程=速度×时间

　　相遇路程=速度和×相遇时间

　　追及路程=速度差×追及时间

　　37.工程问题

　　工作效率×工作时间=1（工作总量）

　　38.不等式的概念

　　41.不等式的基本性质与等式的基本性质的关系

　　①相同点：不论是等式还是不等式，都可以在它的两边加上（或减去）同一个数（式子）。

　　②不同点：等式在两边乘以（除以）同一个正数或同一个负数，等式成立；

　　不等式在两边乘以（除以）同一个正数，方向不变，乘以（除以）同一个负数时，方向一定要改变。

www.youer8.com

　　42.不等式的解的定义

　　能使不等式成立的未知数的值，叫做不等式的解。

　　43.不等式的解集的定义

　　一个含有未知数的不等式的解的全体叫做不等式的解集。

　　44.解不等式

　　求不等式解集的过程叫做解不等式。

　　解不等式的依据：不等式的三条性质，特别是不等式的性质3，注意不等号方向的改变。

　　45.如何用数轴表示不等式的解集

　　一是确定“界点”:解集包含“界点”则用实心圆点；反之，空心圆圈。

　　二是确定“方向”:大于向右画，小于向左画。

　　46.一元一次不等式组的概念

　　由几个含有同一个未知数的一次不等式组成的不等式组。

　　47.一元一次不等式组的解集的概念

　　一元一次不等式组中各个不等式的解集的公共部分，叫这个一元一次不等式组的解集。

　　解集的公共部分通常用“数轴”来确定。

　　解集规律：大大取大；小小取小；大小小大中间找；大大小小是无解。

　　48.不等式组的解法

　　①求出不等式组中各个不等式的解集；②在数轴上表示各个不等式的解集；

　　③确定各个不等式解集的公共部分即这个不等式组的解集。

　　49.一元一次不等式组的应用

　　与列方程解应用题类似，列不等式（组）解应用题，求出的通常是一个量的取值范围。

　　50.二元一次方程

　　含有两个未知数的一次方程叫做二元一次方程。
　　

上一篇：上海预初第二学期数学知识点（一）